Subspace Mixed Finite Elements for Real-Time Heterogeneous Elastodynamics
SessionDeformable Solids
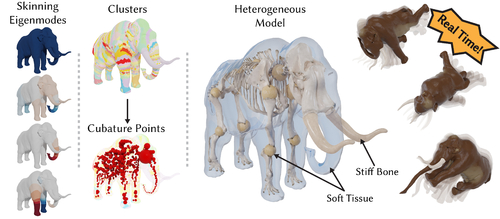
DescriptionReal-time elastodynamic solvers are well-suited for the rapid simulation of ho
mogeneous elastic materials, with high-rates generally enabled by aggressive
early termination of timestep solves. Unfortunately, the introduction of strong
domain heterogeneities can make these solvers slow to converge. Stopping the
solve short creates visible damping artifacts and rotational errors. To address
these challenges we develop a reduced mixed finite element solver that pre
serves rich rotational motion, even at low-iteration regimes. Specifically, this
solver augments time-step solve optimizations with auxillary stretch degrees
of freedom at mesh elements, and maintains consistency with the primary
positional degrees of freedoms at mesh nodes via explicit constraints. We make
use of a Skinning Eigenmode subspace for our positional degrees of freedom.
We accelerate integration of non-linear elastic energies with a cubature approx
imation, placing stretch degrees of freedom at cubature points. Across a wide
range of examples we demonstrate that this subspace is particularly well suited
for heterogeneous material simulation. Our resulting method is a subspace
mixed finite element method completely decoupled from the resolution of the
mesh that is well-suited for real-time simulation of heterogeneous domains.
mogeneous elastic materials, with high-rates generally enabled by aggressive
early termination of timestep solves. Unfortunately, the introduction of strong
domain heterogeneities can make these solvers slow to converge. Stopping the
solve short creates visible damping artifacts and rotational errors. To address
these challenges we develop a reduced mixed finite element solver that pre
serves rich rotational motion, even at low-iteration regimes. Specifically, this
solver augments time-step solve optimizations with auxillary stretch degrees
of freedom at mesh elements, and maintains consistency with the primary
positional degrees of freedoms at mesh nodes via explicit constraints. We make
use of a Skinning Eigenmode subspace for our positional degrees of freedom.
We accelerate integration of non-linear elastic energies with a cubature approx
imation, placing stretch degrees of freedom at cubature points. Across a wide
range of examples we demonstrate that this subspace is particularly well suited
for heterogeneous material simulation. Our resulting method is a subspace
mixed finite element method completely decoupled from the resolution of the
mesh that is well-suited for real-time simulation of heterogeneous domains.
Event Type
Technical Papers
TimeFriday, 15 December 20232:40pm - 2:50pm
LocationMeeting Room C4.8, Level 4 (Convention Centre)



